Skip to main content
TU-Clausthal Institute of Physical Chemistry

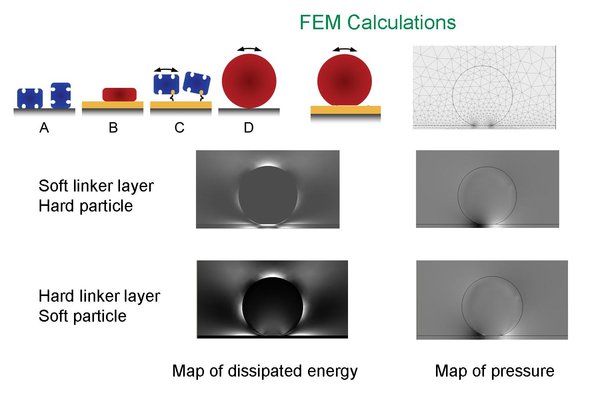
QCM modeling with the finite element method

When the quartz resonator comes into contact with a liquid or a film, the shift in frequency and bandwidth can be predicted using analytical formulas. These can usually be inverted and certain material properties (such as the film thickness) can be derived directly and explicitly. Such formulas do not exist for complicated samples, but the shift in frequency and attenuation can still be derived numerically.

We use the finite element method to calculate the area-averaged lateral stress that the sample exerts on the crystal. This stress is proportional to the frequency shift. Such models are also interesting in that the pressure distribution in the sample or the distribution of the dissipated energy in the sample can also be obtained as a result of the modeling.

Literature

  • Pomorska, A.; Shchukin, D.; Hammond, R.; Cooper, M. A.; Grundmeier, G.; Johannsmann, D.
    Positive Frequency Shifts Observed Upon Adsorbing Micron-Sized Solid Objects to a Quartz Crystal Microbalance from the Liquid Phase.
    Analytical Chemistry2010, 82, (6), 2237-2242.
  • Johannsmann, D.; Reviakine, I.; Richter, R. P.
    Dissipation in Films of Adsorbed Nanospheres Studied by Quartz Crystal Microbalance (QCM).
    Analytical Chem istry 2009, 81, (19), 8167-8176.
  • Johannsmann, D.; Reviakine, I.; Rojas, E.; Gallego, M.
    Effect of Sample Heterogeneity on the Interpretation of QCM(-D) Data: Comparison of Combined Quartz Crystal Microbalance/Atomic Force Microscopy Measurements with Finite Element Method Modeling.
    Analytical Chem istry 2008, 80, (23), 8891-8899.