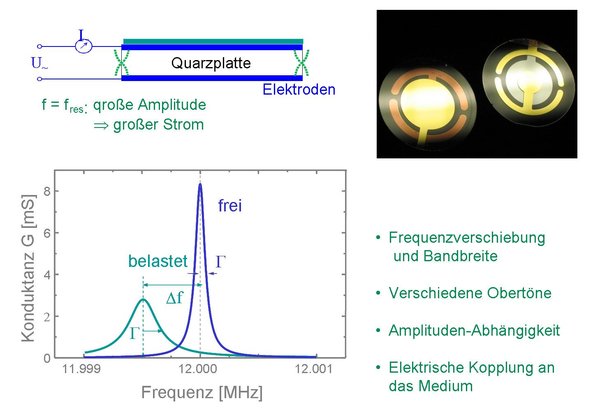
The quartz crystal microbalance is considered an extraordinarily simple device. A small piezoelectric disk is excited to a thickness shear oscillation by an AC voltage of MHz. If the AC voltage matches the acoustic resonance frequency of the disk, then the shear amplitude (and at the same time the current through the electrodes) becomes very high.This makes it very easy to detect an acoustic resonance electrically. This resonance is sharper than anything known from electrical oscillating circuits. This is why oscillating crystals are the clock generators in many watches.

When the crystal comes into contact with a sample, the resonance frequency shifts. If, for example, the sample is a thin film, the frequency shift is proportional to the film thickness and the film thickness (more precisely the mass of the film in units of ^g/cm2) can be determined. This device is the quartz crystal microbalance.

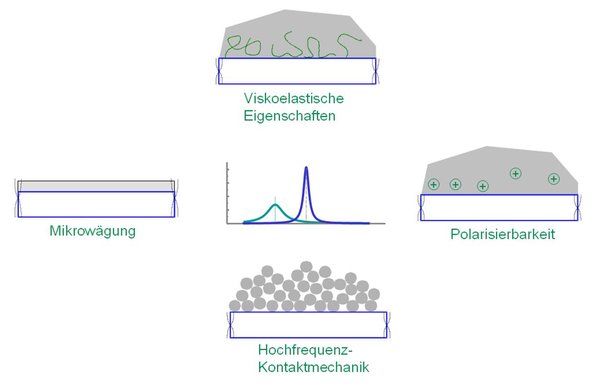
But what if the sample is not a thin film, but a biofilm, a pile of sand, a gel or a foam? Then the Sauerbrey equation alone does not help. However, we can obtain even more information about the sample from the oscillating quartz microbalance via the frequency shift alone. These are

• The bandwidth of the resonance
• Frequency shifts and bandwidths on different harmonics
• The dependence of the frequency and bandwidth on the vibration amplitude
• The dependence of frequency and bandwidth on the grounding of the front electrode

Furthermore, the oscillating quartz microbalance is often combined with other instruments for surface analysis, for example the atomic force microscope, electrochemical cyclic voltammetry or surface plasmon microscopy.

Central to the analysis is the "small load approximation". As long as the frequency shift is much smaller than the frequency itself, the frequency shift Δf is proportional to the in-phase component of the lateral stress at the surface of the disk. The bandwidth is proportional to the out-of-phase component of the stress. These stresses can also be calculated numerically for complex samples, e.g. using the finite element method.

We are currently particularly interested in high-frequency contact mechanics, which we are investigating with quartz resonators. Here are papers on the analysis of viscoelastic modeling of soft samples on quartz resonators.